Javascriptでcubic-bezierを計算する

【祝日・不定期限定】なんでも相談できる特別プラン16,500円、特別クーポン40%引きを数量限定で実施します！猛暑が続いている間実施します！まずはご相談ください！

1970/01/01
2021/01/14

概要

CSS の transition プロパティで使える cubic-bezier 関数を使うことは良くあると思います。
しかし、Javascript ではどうでしょうか？使ったことがないという方が多いでしょう。

Javascript の標準関数には cubic-bezier (3次のベジュ曲線) と等価なものはありません。
そのため自作しなければならないのですが、Web 上ではなかなか紹介されていません。

そこで cubic-bezier を計算する関数を生成する関数を作ったので紹介します。

cubic-bezierは制御点が4つの3次ベジュ曲線

cubic-bezier について簡単に説明しておきます。

CSS の transition-timing-function プロパティ以外でも、SVG のパスや Microsoft Office の曲線ツール (頂点の編集)、Adobe Illustrator の曲線ツールなどに代表されるベクター画像を生成する際に広く利用されています。
始点と終点をつなぐ様々な曲線を表現できコンピュータで処理する曲線には最適です。

cubic-bezier 関数は4つの引数 (2つの制御点の座標) を持ち、始点である (0, 0) 座標から終点の (1, 1) 座標をつなぐ曲線を生成します。
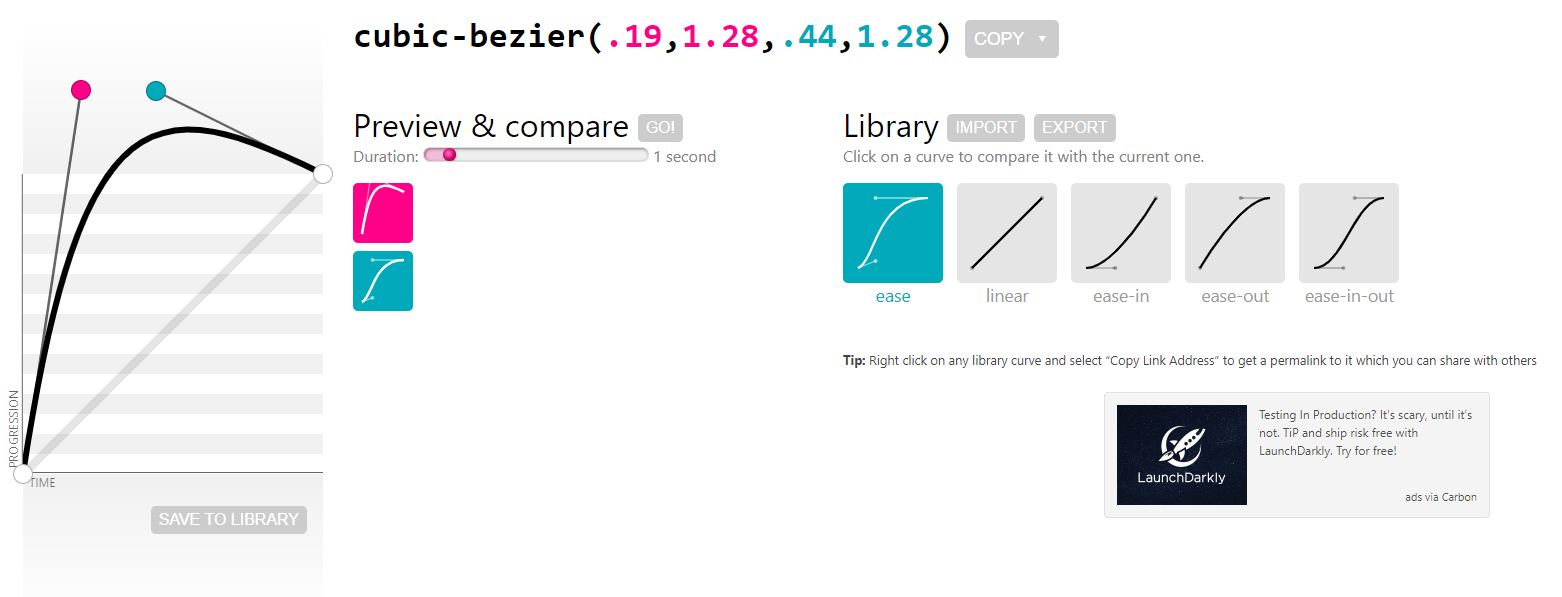
どんな曲線が作られるのかは以下のサイトが非常に分かりやすいのでご自分の手で制御点を動かして試してみて下さい。
transition した際の変移の仕方もアニメーションさせてプレビューできます。

cubic-bezier.com

Javascriptで実装したコード

では、さっそく Javascript で実装したコードを以下に示します。

// Cubic-Bezierの値を計算する関数を生成する関数

var cubicBezier = function($x1, $y1, $x2, $y2){

// Refer: http://www.moshplant.com/direct-or/bezier/math.html

var cx = 3 * $x1,

bx = 3 * ($x2 - $x1) - cx,

ax = 1 - cx - bx;

var cy = 3 * $y1,

by = 3 * ($y2 - $y1) - cy,

ay = 1 - cy - by;

// 媒介変数表示したX座標

var bezierX = function ($t) {

return $t * (cx + $t * (bx + $t * ax));

};

// X座標のt微分

var bezierDX = function($t){

return cx + $t * (2 * bx + 3 * ax * $t);

};

// ニュートン法で数値解析する

var newtonRaphson = function($x){

if($x <= 0){

return 0;

}

if($x >= 1){

return 1;

}

var prev, t = $x;

do{

prev = t;

t = t - ((bezierX(t) - $x) / bezierDX(t));

} while(Math.abs(t - prev) > 1e-4); // 1e-2 程度でも良い

return t;

};

return function($t){

// X座標(時刻)に対応する媒介変数tの値を取得する

var t = newtonRaphson($t);

// Y座標(Easing量)を計算する

return t * (cy + t * (by + t * ay));

};

上記関数を使って cubic-bezier が返す値を計算する関数を生成します。
この時、生成した関数の引数には0～1で正規化した値を与えます。

// Easing関数を生成

var easeOvershoot = cubicBezier(0.13, 0.51, 0.57, 3.24);

var easeNormal = cubicBezier(0.25, 0.1 , 0.25, 1.0 ); // CSSのtransitionのtiming-function初期値

// Easingの値を取得

console.log(easeOvershoot(0.5));

console.log(easeNormal(0.5));

コードの簡単な説明

まずは媒介変数表示にした際の曲線を求めます。
x = x(t), y = y(t) という形です。
X座標とY座標は独立して求めることができます。それぞれ同じ形の式になります。(詳しいことは自分で考えて下さい)
参考 URL 先に計算した式があるのでこちらを使いましょう。

The Math Behind the Bézier Curve

ここで、X座標は Easing 関数の時刻にあたります。
そこで x(t) を解いて x に対応する媒介変数の値 t を求める必要があります。
x(t) は3次関数なので解析的に解くことも可能です。
但し、3乗根を計算したり煩雑な式になるのでここでは数値解析を行うこととします。

主にアニメーションで使用すると思う (違う方は厳密解を求めて下さい) ので大体の値が求まれば良いです。
そこでニュートン法を用いて数値的に解析することにします。この方がコードがずっとスッキリします。
数値解析により媒介変数の値が求まるのでこれを使ってY座標の値を計算しています。

まとめ

以上、Javascript で cubic-bezier を求める方法でした。
Canvas などでアニメーションする際に Easing したい際などにはぜひご利用下さい。

※メールアドレスは表示されません。(2019/07/11変更) ※短時間で連続してのコメントはできません。 ※いたずら防止のために IP アドレスを記録しています。ご了承願います。

きのぴーさん (ID：3o9l4x) 投稿日時：2022-03-23 12:47:49

WallpaperEngineというソフトでスクリプトベースでアニメーションを作らせていただいているのですが、大変参考になりました！！
どうやってlinearとかの加速度的に増えていく運動量を計算すればいいんだろうと頭悩ませていたのですが、上記のコードを使って運動量とかを正規化してあげたら一気にできるようになりました！